6/3, Tree, Morris 遍历
这个帖子的描述和代码非常好,还有这个。
我一开始以为 Morris 遍历会改变原树的结构所以不能用,后来发现并不会。。。于是这种技巧还是很值得掌握的。
1968年,Knuth提出说能否将该问题的空间复杂度压缩到O(1),同时原树的结构不能改变。大约十年后,1979年,Morris在《Traversing Binary Trees Simply and Cheaply》这篇论文中用一种Threaded Binary Tree的方法解决了该问题。
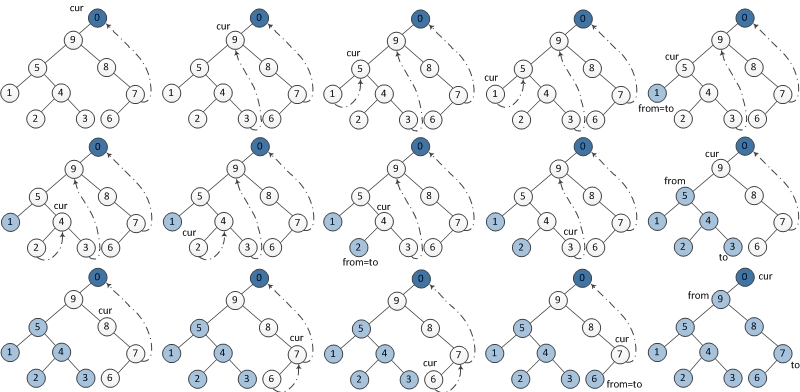
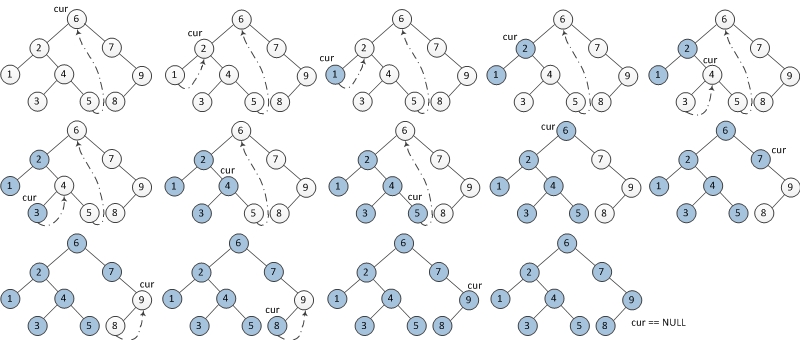
每次访问root左子树之前,先找到左子树里面最右面的点,并把其 right 指针连到 root 上;左子树遍历完这个点之后,再把这个多出来的指针拆掉。
Morris in-order 流程,利用 threaded binary tree.
public class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
TreeNode cur = root;
while(cur != null){
if(cur.left == null){
list.add(cur.val);
cur = cur.right;
} else {
TreeNode prev = cur.left;
while(prev.right != null && prev.right != cur){
prev = prev.right;
}
if(prev.right == null){
prev.right = cur;
// Uncomment for pre-order 第一次到中间节点
// list.add(cur.val);
cur = cur.left;
} else {
prev.right = null;
// Uncomment for in-order, 左边结束到中间节点
// list.add(cur.val);
cur = cur.right;
}
}
}
return list;
}
}
Morris 的 post-order 遍历还要建一个 dummy node 以及反序输出。。感觉不是非常现实。。。有空复习的时候我再研究研究这种 trick 吧。