7/5, Interval 类，扫描线

Interval 类问题中最常用的技巧，就是自定义 IntervalComparator，把输入按照 startTime 升序排序。

对于任意两个区间A与B，如果

A.end > B.start 并且
A.start < B.end
则 A 与 B 重叠。

按 start 排序后，数组有了单调性，上面的判断条件就简化成了 A.end > B.start 则一定重叠.

排序后的 Interval 扫描过程中，为了保证正确性，要格外小心多个 Interval 在同一 x 时，处理的先后顺序，比如 skyline problem.

熟悉下 TreeMap 的常用 API.

get()

put()

containsKey()

size()

values() : 返回 Collection<> of V

lowerKey(K key) ：返回最大的小于参数的Key，没有则 null

higherKey(K key)：返回最小的大于参数的Key, 没有则 null

firstKey() : 返回最小 key

lastKey() : 返回最大 key

coursera 上Princeton Week5 公开课不错

Meeting Rooms

Trivial Problem.

public class Solution {
    private class IntervalComparator implements Comparator<Interval>{
        public int compare(Interval a, Interval b){
            return a.start - b.start;
        }
    }

    public boolean canAttendMeetings(Interval[] intervals) {
        if(intervals == null || intervals.length <= 1) return true;

        Arrays.sort(intervals, new IntervalComparator());

        for(int i = 1; i < intervals.length; i++){
            if(intervals[i].start < intervals[i - 1].end) return false;

        }

        return true;
    }
}

如果已经知道end time最大, 可以建立array, count[start]++, count[end]--, 任一时刻如果count[i]>1, 返回false.

Meeting Rooms II

fb 面经高频题，follow up 是返回那个 overlap 最多的区间。

扫描线算法。需要注意的是如果有两个 interval 首尾相接，要把结束的那个排在 array 的前面，先把房间腾出来；否则的话会认为收尾相接的两个 meeting 需要占 2 个房间，这是错误的。

[[0, 30],[5, 10],[15, 20]]

(0,true) (5, true) (10, false) (15, true) (20, false) (30, false)

public class Solution {
    private class Point{
        int time;
        boolean isStart;
        public Point(int time, boolean isStart){
            this.time = time;
            this.isStart = isStart;
        }
    }

    private class PointComparator implements Comparator<Point>{
        public int compare(Point a, Point b){
            if(a.time == b.time) return a.isStart ? 1 : -1 ;
            else return a.time - b.time;
        }
    }

    public int minMeetingRooms(Interval[] intervals) {
        if(intervals == null || intervals.length == 0) return 0;

        Point[] arr = new Point[intervals.length * 2];

        for(int i = 0; i < intervals.length; i++){
            arr[i * 2] = new Point(intervals[i].start, true);
            arr[i * 2 + 1] = new Point(intervals[i].end, false);
        }

        Arrays.sort(arr, new PointComparator());

        int maxOverLap = 0;
        int curCount = 0;
        for(Point pt : arr){
            if(pt.isStart) curCount ++;
            else curCount --;
            maxOverLap = Math.max(maxOverLap, curCount);
        }

        return maxOverLap;
    }
}

还有一种做法是维护priority queue

    public int minMeetingRooms(Interval[] intervals){
        if(intervals==null) return 0;
        if(intervals.length<=1) return intervals.length;
        Arrays.sort(intervals, new Comparator<Interval>(){
            public int compare(Interval i1, Interval i2){
                if(i1.start == i2.start)
                    return i1.end-i2.end;
                return i1.start - i2.start;
            }
        });

        PriorityQueue<Integer> pq = new PriorityQueue<Integer>();
        int num = 1;
        pq.offer(intervals[0].end);
        for(int i=1;i<intervals.length;i++){
            if(intervals[i].start>=pq.peek()){
                pq.poll();
                pq.offer(intervals[i].end);
            }
            else{
                num++;
                pq.offer(intervals[i].end);
            }
        }
        return num;

    }

(FB) follow-up: 如何返回重叠最多的那个区间？

当前 maxOverlap 创造新高的时候，存下 start 的时间戳，因为这是所有重合区间中 start 时间最晚的一个；
继续扫描，看到新的 end 的时候，存下这个 end 的时间戳，因为它是重合区间里 end 时间最早的一个；
二者之间，就是具体的 max overlap 区间

另一个fb onsite 面经题里，首先给 n 个一维 interval，返回任意重合最多的点；然后给 n 个二维 rectangle，返回任意重复最多的点。

按照2n 个y把y划分成2n-1个区间，每个区间在做一位的算法（covered by most intervers）

时间复杂度 n^2log(n)

https://www.cs.princeton.edu/~rs/AlgsDS07/17GeometricSearch.pdf

https://www.coursera.org/learn/algorithms-part1/lecture/mNiwq/rectangle-intersection

Merge Intervals

这题需要注意的 corner case 有两个：

按 startTime 排序后， merge 的新 interval 可能是完全包含于前一个 interval 的，如【1,4】，【2,3】. 所以当发现 overlap 时，新的 End 要以两个 end 的最大值为准。
记得循环尾部做一个收尾，把最后 merge 完的结果生成新的 interval 也加到 list 中。

  public List<Interval> merge(List<Interval> intervals) {
    List<Interval> result = new ArrayList<Interval>();

    if(intervals==null||intervals.size()==0)
        return result;

    Collections.sort(intervals, new Comparator<Interval>(){
        public int compare(Interval i1, Interval i2){
            if(i1.start!=i2.start)
                return i1.start-i2.start;
            else
                return i1.end-i2.end;
        }
    });

    Interval pre = intervals.get(0);
    for(int i=1; i<intervals.size(); i++){
        Interval curr = intervals.get(i);
        if(curr.start>pre.end){
            result.add(pre);
            pre = curr;
        }else{
            Interval merged = new Interval(pre.start, Math.max(pre.end, curr.end));
            pre = merged;
        }
    }
    result.add(pre);

    return result;
}

Insert Interval

顺着上一题的思路，一个最简单直接的写法就是。。直接把新的 interval 插进去，然后再跑一遍 merge interval 的代码。

考虑到一些极端情况，比如 newInterval 合并了原始 list 中绝大多数 intervals, 在原 list 上进行操作的话需要的比较与删减也会很多，所以从算法复杂度上讲，这种写法至少可以 AC，但不是最优。

三种情况

不相交, new.end<cur.start---->add new interval, new interval=cur interval

不相交, new.start>cur.end-----> add cur Interval, continue

有overlap, new完全包含cur, cur完全包含new, cur new部分包含彼此 ----->new Interval(minstart, maxend)

public class Solution {
    public List<Interval> insert(List<Interval> intervals, Interval newInterval) {

        List<Interval> result = new ArrayList<Interval>();

        for(Interval interval: intervals){
            if(interval.end < newInterval.start){
                result.add(interval);
            }else if(interval.start > newInterval.end){
                result.add(newInterval);
                newInterval = interval;        
            }else{
                newInterval = new Interval(Math.min(interval.start, newInterval.start), Math.max(newInterval.end, interval.end));
            }
        }

        result.add(newInterval); 

        return result;
    }
}

在此基础上还可以进一步优化，不用额外空间，on-the-fly 解决战斗。

这种做法可以不花费任何额外空间，但是时间复杂度会更高，因为 List.remove() 是一个 O(n) 操作，add(index, val) 也是 O(n) 的。

 public List<Interval> insert(List<Interval> intervals, Interval newInterval) {
        int ptr = 0;

        while(ptr < intervals.size() && intervals.get(ptr).end < newInterval.start) ptr++;
        while(ptr < intervals.size() && intervals.get(ptr).start <= newInterval.end){
            newInterval.start = Math.min(newInterval.start, intervals.get(ptr).start);
            newInterval.end = Math.max(newInterval.end, intervals.get(ptr).end);
            intervals.remove(ptr);
        }
        intervals.add(ptr, newInterval);

        return intervals;
    }

Summary Ranges

一个比较简单的区间融合问题

public class Solution {
    public List<String> summaryRanges(int[] nums) {
        List<String> list = new ArrayList<String>();
        if(nums.length==0) return list;
        int start = nums[0]; int end = nums[0]; int expect = start+1;
        for(int i=1;i<nums.length;i++){
            if(nums[i]==expect){
                expect++; end = nums[i];
            }
            else{
                StringBuilder sb = new StringBuilder();
                if(start==end)
                    sb.append(start);
                else
                    sb.append(start+"->"+end);
                list.add(sb.toString());
                start = nums[i]; end = nums[i]; expect = start+1;
            }
        }
        StringBuilder sb = new StringBuilder();
        if(start==end)
            sb.append(start);
        else
            sb.append(start+"->"+end);
        list.add(sb.toString());
        return list;
    }
}

第一种不太经济的写法是，建一个 boolean[upper - lower + 1] ，扫一遍数组记录下每个数是否出现过，然后根据 boolean[] 的 flag 进行融合。这种写法首先需要 O(upper - lower) 的 extra space，而且最重要的是，没有利用到原数组 int[] 已经是排序了的性质，因此速度上不给力，而且在 upper = 100000000, lower = -10000000 这种极端情况下，空间占用非常大。

改进后的代码实现过程中，最开始没有考虑全 test case，虽然AC 了但是代码不够 clean. 下面参考论坛里的解法就简明了很多。

如果实现代码的时候发现要写很多 if else 处理特殊情况，最好的选择还是暂停一下，多把 test case 思考全再动手。

39/40 passed, 挂在了 -2147483648 2147483647

public class Solution {
    public List<String> findMissingRanges(int[] nums, int lower, int upper) {
        List<String> list = new ArrayList<String>();

        int expect = lower;
        for(int i=0;i<nums.length;i++){
            if(i>0&&nums[i-1]==nums[i]) continue;
           if(nums[i]==expect){
                expect++;
                continue;
            }

            int start = expect; int end = nums[i]-1;
            if(start==end) list.add(start+"");
            else list.add(start+"->"+end);

            expect = nums[i]+1;
        }
        int last = nums.length==0? lower-1: nums[nums.length-1];
        if(last!=upper){
            if(last+1==upper) list.add(upper+"");
            else list.add((last+1)+"->"+upper);
        }
        return list;
    }
}

【lower, nums[i] - 1】范围内没有数, ADD;

【nums[last] + 1，upper】范围内没有数, ADD;
动态更新 lower，维护当前有效 range.

时间复杂度 O(n).

public List<String> findMissingRanges(int[] nums, int lower, int upper) {
        List<String> res = new ArrayList<>();
        long Lower = (long)lower;
        long Upper = (long)upper;
        for (int num : nums) {
            long justBelow = (long)num - 1;
            if (justBelow == Lower) res.add(String.valueOf(justBelow));
            else if (justBelow > Lower) res.add(Lower + "->" + justBelow);
            if (num == Integer.MAX_VALUE) return res;
            Lower = (long)num + 1; 
        }
        if (Lower == Upper) res.add(String.valueOf(Upper));
        else if (Lower < Upper) res.add(Lower + "->" + Upper);
        return res;
    }
}

Data Stream as Disjoint Intervals

参考了论坛代码之后，另一种巧妙的做法：

addNum(int val) 时间复杂度：O(log n)

getIntervals() 时间复杂度：o(n log n) ?? should be O(n)

空间复杂度： O(n)

如果num存在, 返回
add num then merge with lowkey and highkey, remove highkey
add num then merge with lowkey
add num then merge with highkey, put treemap (num, new Interval(num, end)), remove highkey;
add num and don't merge

public class SummaryRanges {
    TreeMap<Integer, Interval> map;
    /** Initialize your data structure here. */
    public SummaryRanges() {
        map= new TreeMap<Integer, Interval>();
    }

    public void addNum(int val) {
        if(map.containsKey(val))
            return;
        else{
            Integer lk = map.lowerKey(val);
            Integer hk = map.higherKey(val);
            if(lk!=null && hk!=null && map.get(lk).end+1== val && hk==val+1){
                map.get(lk).end = map.get(hk).end;
                map.remove(hk);
            }
            else if(lk!=null && map.get(lk).end+1>=val){
                map.get(lk).end = Math.max(val, map.get(lk).end);
            }
            else if(hk!=null && hk==val+1){
                map.put(val, new Interval(val, map.get(hk).end));
                map.remove(hk);
            }
            else
                map.put(val, new Interval(val, val));
        }
    }

    public List<Interval> getIntervals() {
        return new ArrayList<Interval>(map.values());
    }
}

(FB) 给定的是 stream of intervals，求 cover range.

这么改了之后难了很多。。用 TreeMap 依然可以，但是假设目前 TreeMap 维护的都是 none-overlapping intervals，一个新 interval 加入之后可能会出现若干种情况：

完全被某个 interval 包含，无影响；
完全和其他 interval disjoint，插入即可；
和左边的 overlap，但是不和右边的 overlap;
和右边的 overlap，但是不和左边的 overlap;
一次跨了多个 interval，这里面就有全包括的，包括一半的，在左边搭边的，在右边搭边的。。。

于是我觉得这题用 TreeMap 比较和乎人性的做法是，TreeMap 只负责维护 sorted intervals，需要查询 coverage 的时候，直接 new ArrayList<>(treeMap.values()) 给导出来然后跑一遍 merge interval ..

或者，直接维护一个按照 start time 排好序的 disjoint list of intervals，然后每次新的 interval 过来的时候，就 in-place 扫一遍做 merge 好了~ 这样每次 insert O(N)，getCoverage O(1)

The Skyline Problem

扫描线算法，因为 building outline 只可能发生在每一段 "start/end" 的边界上，因此以每个 edge 的 (x, height) 排序，而后扫描。

当 x 值不同时，x 小的排在前面；
else 当 y 值不同时，y 小的排在前面；
- 调换的话下面的代码会有 bug

这题在九章课上讲的时候，使用的是 HashHeap，我们需要一个 maxHeap 来检测对于每一个点，我们建筑的最大高度，但同时在扫描过程中我们需要对每一个具体的 edge 进行删除操作，而 HashHeap 可以做到 O(log n) 的复杂度，Java 默认的 heap 只能做到 O(n).

如何在 heap 中快速删除这个问题和当初准备 Bloomberg 时候的马拉松问题一样，Java 中有现成的解决方案：

TreeMap.

接下来的问题是：

当遇到一座楼的右边界时，如何删除其对应的左边界？在 TreeMap 里直接用 Edge class 做 key 是不行的，因为我们无法通过 new 一个参数一模一样的 instance 去做 lookup. 所以在 Key-Value 的设计中，我们应该用 height 做 Key，因为同一座建筑左右墙 height 相等，就可以实现查找。即使有多座 height 一样的左墙，我们也只需要用 count 做 value，把当前 height 的墙数减一即可。
对于同一高度的不同建筑，如何确保其在 TreeMap 中不会互相 replace ，从而保证算法的正确性? 在自己 debug 的过程中，即使后面逻辑完全一致，不用负数 height 做 Key 依然会有 bug. ，用负数可以省去 Edge class 里面一个变量，最主要的是，在调用 Arrays.sort() 时，可以保证对于同一个 x 位置，在增加时永远先处理 height 最高的建筑，而删除时永远先删除 height 最小的建筑，从而保证了在同一个高度上多个建筑 Edge 重叠时，算法的正确性。
如何正确处理建筑清光之后，剩余高度为 0 的情况？一开始在 TreeMap 里加一个 (0, 1) 的 entry，代表始终有一个高度为 0 的墙，即地面；

O(Edge 排序) + O(Edge 数 * (插入 / 删除 + 查找))

O(2n log 2n) + O(2n * (log 2n + log 2n)) = O(n log n)

public class Solution {
    private class Edge implements Comparable<Edge>{
        int x;
        int y;

        public Edge(int x, int y){
            this.x = x;
            this.y = y;
        }

        public int compareTo(Edge b){
            // Ascending in x coordinate
            if(this.x != b.x) return this.x - b.x;
            else return this.y - b.y;
        }
    }

    public List<int[]> getSkyline(int[][] buildings) {
        // Key : height of edge
        // Value : count of edges of that height
        TreeMap<Integer, Integer> treeMap = new TreeMap<>();
        List<int[]> list = new ArrayList<>();
        Edge[] edges = new Edge[2 * buildings.length];

        for(int i = 0; i < buildings.length; i++){
            int[] building = buildings[i];
            edges[i * 2] = new Edge(building[0], -building[2]);
            edges[i * 2 + 1] = new Edge(building[1], building[2]);
        }

        Arrays.sort(edges);
        treeMap.put(0, 1);
        int prevHeight = 0;

        for(Edge edge : edges){
            if(edge.y < 0){
                if(!treeMap.containsKey(-edge.y)){
                    treeMap.put(-edge.y, 1);
                } else {
                    int count = treeMap.get(-edge.y);
                    treeMap.put(-edge.y, count + 1);
                }
            } else {
                int count = treeMap.get(edge.y);
                if(count == 1){
                    treeMap.remove(edge.y);
                } else {
                    treeMap.put(edge.y, count - 1);
                }
            }

            int curHeight = treeMap.lastKey();
            if(prevHeight != curHeight){
                list.add(new int[]{edge.x, curHeight});
                prevHeight = curHeight;
            }
        }

        return list;
    }
}

当 x 值不同时，x 小的排在前面；
else 当 y 值不同时，y 小的排在前面；
- 调换的话下面的代码会有 bug, input: [[0,2,3],[2,5,3]] output: [[0,3],[2,0],[2,3],[5,0]] expected: [[0,3],[5,0]]
- 原因是相邻等高的边, 会先弹出右边, 再加入左边, 这样多了两个点
PQ要先offer(0)这个地板. 为了最后一个点
(O(n^2)time, O(n) space)

public class Solution {
    public List<int[]> getSkyline(int[][] buildings) {
        List<int[]> ans = new ArrayList<int[]>();
        List<int[]> height = new ArrayList<int[]>();
        for(int h[]:buildings){
            height.add(new int[]{h[0],-h[2]});
            height.add(new int[]{h[1],h[2]});
        }
        Collections.sort(height, new Comparator<int[]>(){ 
            public int compare(int[] a, int b[]){
                if(a[0]!=b[0]) return a[0]-b[0];
                return b[1]-a[1];
            }
        });

        PriorityQueue<Integer> pq = new PriorityQueue<Integer>(Collections.reverseOrder());
        pq.offer(0);//skylin最后一个点高度总是0; cur = pq.peek() pq为空当最后一个点remove时
        int prev = -1;
        for(int[] h : height){
            if(h[1]<0){
                pq.offer(-h[1]);
            }
            else
                pq.remove(h[1]);
            int cur = pq.peek();
            if(cur!=prev){
                ans.add(new int[]{h[0], cur});
                prev = cur;
            }
        }
        return ans;
    }
}

Rectangle Area (G)

这道题LeetCode问的是两个，简单的math可以解决。overlap部分一定是两个长方形的左下x,y最大值和两个长方形右上的最小值计算的。当最大值和最小值valid的时候，overlap是存在的。

public class Solution {
    public int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int x1 = Math.max(A,E);
        int y1 = Math.max(B,F);

        int x2 = Math.min(C,G);
        int y2 = Math.min(D,H);

        int ol = 0;
        if(x2<=x1 || y2<=y1) ol = 0;
        else ol = (x2-x1)*(y2-y1);

        return (C-A)*(D-B) + (G-E)*(H-F) - ol;
    }
}

G问的是N个rectangle求面积。

第二轮, n个矩阵没有三个及以上相交的情况。也就是说面积部分最多属于两个矩阵。

首先对所有矩阵按照左下的x value进行排序，依次扫每个长方形，扫到一个长方形，加入这个长方形的面积。计算当前长方形和上个长方形的overlap，减去overlap。计算overlap的方式和LC尔尔散一样。

高人解答

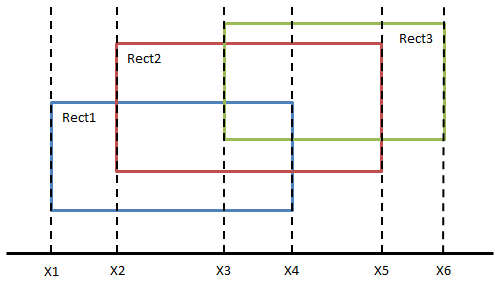
二维长方形求overlap，总面积的思路都在将二维转到一维range；一维range的问题如Interval和skyline转到“点”上。

这个题，

首先根据x value对rectangle 排序，
求每个x value range<x1, x2> <x2, x3>,求出当前range 里y的range。比如插入(x1, <<y1, y2>>) (x2,<<y3,y4>>), (x3, <<y5,y6>>)
对y range进行排序merge
分别求<x1, x2> <x2, x3> 里长方形的和，再累加. 比如(x2-x1)*(y2-y1), (x3-x4)*((y2-y1)+(y3-y4))
对于右边界，注意移除。比如(x4, <<y1,y2>>) 或者每次都get新的Range Y list。

7/5, Interval 类，扫描线

Interval 类问题中最常用的技巧，就是自定义 IntervalComparator，把输入按照 startTime 升序排序。

对于任意两个区间A与B，如果

A.end > B.start 并且

A.start < B.end

则 A 与 B 重叠。

按 start 排序后，数组有了单调性，上面的判断条件就简化成了 A.end > B.start 则一定重叠.

排序后的 Interval 扫描过程中，为了保证正确性，要格外小心多个 Interval 在同一 x 时，处理的先后顺序，比如 skyline problem.

熟悉下 TreeMap 的常用 API.

get()

put()

containsKey()

size()

values() : 返回 Collection<> of V

lowerKey(K key) ： 返回最大的小于参数的Key，没有则 null

higherKey(K key)：返回最小的大于参数的Key, 没有则 null

firstKey() : 返回最小 key

lastKey() : 返回最大 key

coursera 上Princeton Week5 公开课不错

扫描线算法。需要注意的是如果有两个 interval 首尾相接，要把结束的那个排在 array 的前面，先把房间腾出来；否则的话会认为收尾相接的两个 meeting 需要占 2 个房间，这是错误的。

(FB) follow-up: 如何返回重叠最多的那个区间？

当前 maxOverlap 创造新高的时候，存下 start 的时间戳，因为这是所有重合区间中 start 时间最晚的一个；

继续扫描，看到新的 end 的时候，存下这个 end 的时间戳，因为它是重合区间里 end 时间最早的一个；

二者之间，就是具体的 max overlap 区间

另一个fb onsite 面经题里，首先给 n 个一维 interval，返回任意重合最多的点；然后给 n 个二维 rectangle，返回任意重复最多的点。

这题需要注意的 corner case 有两个：

按 startTime 排序后， merge 的新 interval 可能是完全包含于前一个 interval 的，如 【1,4】，【2,3】. 所以当发现 overlap 时，新的 End 要以两个 end 的最大值为准。

记得循环尾部做一个收尾，把最后 merge 完的结果生成新的 interval 也加到 list 中。

三种情况

不相交, new.end<cur.start---->add new interval, new interval=cur interval

不相交, new.start>cur.end-----> add cur Interval, continue

有overlap, new完全包含cur, cur完全包含new, cur new部分包含彼此 ----->new Interval(minstart, maxend)

在此基础上还可以进一步优化，不用额外空间，on-the-fly 解决战斗。

这种做法可以不花费任何额外空间，但是时间复杂度会更高，因为 List.remove() 是一个 O(n) 操作，add(index, val) 也是 O(n) 的。

如果实现代码的时候发现要写很多 if else 处理特殊情况，最好的选择还是暂停一下，多把 test case 思考全再动手。

【lower, nums[i] - 1】 范围内没有数, ADD;

【nums[last] + 1，upper】 范围内没有数, ADD;

动态更新 lower，维护当前有效 range.

时间复杂度 O(n).

参考了论坛代码之后，另一种巧妙的做法：

addNum(int val) 时间复杂度：O(log n)

getIntervals() 时间复杂度：o(n log n) ?? should be O(n)

空间复杂度： O(n)

如果num存在, 返回

add num then merge with lowkey and highkey, remove highkey

add num then merge with lowkey

add num then merge with highkey, put treemap (num, new Interval(num, end)), remove highkey;

add num and don't merge

(FB) 给定的是 stream of intervals，求 cover range.

完全被某个 interval 包含，无影响；

完全和其他 interval disjoint，插入即可；

和左边的 overlap，但是不和右边的 overlap;

和右边的 overlap，但是不和左边的 overlap;

一次跨了多个 interval，这里面就有全包括的，包括一半的，在左边搭边的，在右边搭边的。。。

于是我觉得这题用 TreeMap 比较和乎人性的做法是，TreeMap 只负责维护 sorted intervals，需要查询 coverage 的时候，直接 new ArrayList<>(treeMap.values()) 给导出来然后跑一遍 merge interval ..

或者，直接维护一个按照 start time 排好序的 disjoint list of intervals，然后每次新的 interval 过来的时候，就 in-place 扫一遍做 merge 好了~ 这样每次 insert O(N)，getCoverage O(1)

当 x 值不同时，x 小的排在前面；

else 当 y 值不同时，y 小的排在前面；

调换的话下面的代码会有 bug

TreeMap.

O(Edge 排序) + O(Edge 数 * (插入 / 删除 + 查找))

O(2n log 2n) + O(2n * (log 2n + log 2n)) = O(n log n)

当 x 值不同时，x 小的排在前面；

else 当 y 值不同时，y 小的排在前面；

调换的话下面的代码会有 bug, input: [[0,2,3],[2,5,3]] output: [[0,3],[2,0],[2,3],[5,0]] expected: [[0,3],[5,0]]

原因是相邻等高的边, 会先弹出右边, 再加入左边, 这样多了两个点

PQ要先offer(0)这个地板. 为了最后一个点

(O(n^2)time, O(n) space)

Rectangle Area (G)

这道题LeetCode问的是两个，简单的math可以解决。overlap部分一定是两个长方形的左下x,y最大值和两个长方形右上的最小值计算的。当最大值和最小值valid的时候，overlap是存在的。

第二轮, n个矩阵没有三个及以上相交的情况。也就是说面积部分最多属于两个矩阵。

首先对所有矩阵按照左下的x value进行排序，依次扫每个长方形，扫到一个长方形，加入这个长方形的面积。计算当前长方形和上个长方形的overlap，减去overlap。计算overlap的方式和LC尔尔散一样。

二维长方形求overlap，总面积的思路都在将二维转到一维range；一维range的问题如Interval和skyline转到“点”上。

这个题，

首先根据x value对rectangle 排序，

求每个x value range<x1, x2> <x2, x3>,求出当前range 里y的range。比如插入(x1, <<y1, y2>>) (x2,<<y3,y4>>), (x3, <<y5,y6>>)

对y range进行排序merge

分别求<x1, x2> <x2, x3> 里长方形的和，再累加. 比如(x2-x1)*(y2-y1), (x3-x4)*((y2-y1)+(y3-y4))

对于右边界，注意移除。比如(x4, <<y1,y2>>) 或者每次都get新的Range Y list。

results matching ""

lowerKey(K key) ：返回最大的小于参数的Key，没有则 null

按 startTime 排序后， merge 的新 interval 可能是完全包含于前一个 interval 的，如【1,4】，【2,3】. 所以当发现 overlap 时，新的 End 要以两个 end 的最大值为准。

【lower, nums[i] - 1】范围内没有数, ADD;

【nums[last] + 1，upper】范围内没有数, ADD;

分别求<x1, x2> <x2, x3> 里长方形的和，再累加. 比如(x2-x1)(y2-y1), (x3-x4)((y2-y1)+(y3-y4))