6/14, Two Pointers, Wiggle Sort I & II
Wiggle sort 类问题
如何利用单调性
怎么 partition
什么顺序穿插
如何 in-place
下面这两题 googe 都很喜欢。
Wiggle Sort
首先这题一看就是要你 O(n) 解的,而且要 in-place,不然毫无挑战,因为 quick sort 都 O(n log n)
这题在条件上,比 Wiggle Sort II 要宽松,因此代码变的可以很简单。
wiggle sort 依然利用的数组的单调性,只不过这个单调性每走一步会变一次方向;
如果两对相邻元素有同样的单调性,就不符合题意要求。但是在这种情况下,交换后一对元素的位置,就一定可以得到正确结果。
这题还有一个google面经题变种,在这个帖子中,思想非常类似,更利于思考 wiggle sort 的本质
public class Solution {
public void wiggleSort(int[] nums) {
if (nums.length<=1) return;
for(int i=1;i<nums.length;i++){
if((i%2==1 && nums[i]<nums[i-1]) || (i%2==0 && nums[i]>nums[i-1])){
int tmp = nums[i];
nums[i] = nums[i-1];
nums[i-1] = tmp;
}
}
}
}
Wiggle Sort II
在 Wiggle Sort I 的基础上拿掉了等于号条件,整个题都 gay 了好多,因为这次如果相邻两个数是相等的,怎么 swap 都不符合题意。如果单纯的按顺序扫,就不可避免的会遇到到“找正确元素”的步骤,这个步骤一旦多了,复杂度就上去了。
先写个时间空间都各种不正确的写法,感受下思路。从后往前依次找剩余元素中最大的,按正序插入数组。
有的 test case 是【4,5,5,6】,属于"有重复元素" && "重复元素在第二次遍历插入" && "正好和前一轮结尾相邻" 的情况,所以都正序插入会出 bug.
一种方式是将array先排序以后,依次放入元素。先放大数在奇数位,再放余下数在偶数位。
public class Solution {
public void wiggleSort(int[] nums) {
if (nums.length<=1) return;
Arrays.sort(nums);
//1, 5, 1, 1, 6, 4
//1, 1, 1, 4, 5, 6
//X, 6, X, 5, X, 4
//1, 6, 1, 5, 1, 4
int[] tmp = new int[nums.length];
for(int i=0;i<nums.length;i++)
tmp[i] = nums[i];
int count = nums.length-1;
for(int i=1;i<nums.length;i=i+2){
nums[i] = tmp[count--];
}
for(int i=0;i<nums.length;i=i+2){
nums[i] = tmp[count--];
}
}
}
关于这题,这个帖子写的非常详尽,里面用到了virtual indexing的思想
A(i) = nums[(1+2*(i)) % (n|1)]
(n|1) 强行变奇数。
上面那个 sort 之后从大到小正序穿插插入的顺序,和这题一样,不同之处是,这个写法更符合题目的本质:不需要排序,只需要 partitioning. 正确 partition 的数组只要按照这个顺序插入,都是正确的。
于是问题就分成了三个子问题:
怎么 partitioning
什么顺序穿插
如何 in-place
public void wiggleSort(int[] nums) {
int median = findKthLargest(nums, (nums.length + 1) / 2);
int n = nums.length;
int left = 0, i = 0, right = n - 1;
while (i <= right) {
if (nums[newIndex(i,n)] > median) {
swap(nums, newIndex(left++,n), newIndex(i++,n));
}
else if (nums[newIndex(i,n)] < median) {
swap(nums, newIndex(right--,n), newIndex(i,n));
}
else {
i++;
}
}
}
private int newIndex(int index, int n) {
return (1 + 2*index) % (n | 1);
}
Find Permutation
先上一个错误思路,根据升降序原则得出[0,-1,-2,-1,0,-1,0]这个表格。再根据表格填数,得到[5,2,1,3,6,4,7]这里犯了一个错误是-1不一定需要比0小,非相邻元素不要包含此规定。正解为[3,2,1,4,6,5]
public class Solution {
public int[] findPermutation(String s) {
HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
char[] arr = s.toCharArray();
int[] ans = new int[arr.length+1];
int pre = 0; int min = 0; int max = 0;
for(char c : arr){
map.put(pre, map.getOrDefault(pre,0)+1);
if(c=='D') pre--;
else pre++;
min = Math.min(min, pre);
max = Math.max(max, pre);
}
map.put(pre, map.getOrDefault(pre,0)+1);
int[] start = new int[max-min+1];
int idx = 0; int count = 1;
for(int i=min;i<=max;i++){
if(map.containsKey(i)){
start[idx] = count;
count+=map.get(i);
}
idx++;
}
idx = 0;
ans[0] = start[idx-min]; start[idx-min]++;
for(int i=1;i<ans.length;i++){
char c = s.charAt(i-1);
if(c=='D') idx--;
else idx++;
System.out.println(idx);
System.out.println(min);
ans[i] = start[idx-min];
start[idx-min]++;
}
return ans;
}
}
看了论坛上的答案后,理解了本题本质上就是wigle sort,只不过将连续的‘I’和‘D’看成一个整体。
正确 的打开方式是建立一个升序数组,对连续的‘D’部分reverse。
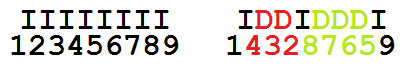
public class Solution {
public int[] findPermutation(String s) {
int[] ans = new int[s.length()+1];
for(int i=0;i<ans.length;i++) ans[i] = i+1;
for(int i=0;i<s.length();i++){
if(s.charAt(i)=='D'){
int low = i;
while(i<s.length() && s.charAt(i)=='D') i++;
int high = i;
i--;
reverse(ans, low, high);
}
}
return ans;
}
public void reverse(int[] ans, int low, int high){
while(low<high){
int tmp = ans[low];
ans[low] = ans [high];
ans[high] = tmp;
low++;high--;
}
}
}