这个帖子讲的很好

最小生成树

带权图分为有向和无向，无向图的最短路径又叫做最小生成树，有prime算法和kruskal算法；有向图的最短路径算法有dijkstra算法和floyd算法。

生成树的概念：联通图G的一个子图如果是一棵包含G的所有顶点的树，则该子图称为G的生成树 生成树是联通图的极小连通子图。所谓极小是指：若在树中任意增加一条边，则 将出现一个回路；若去掉一条边，将会使之编程非连通图。生成树各边的权 值总和称为生成素的权。权最小的生成树称为最小生成树，常用的算法有prime算法和kruskal算法。

最短路径问题旨在寻找图中两节点之间的最短路径，常用的算法有：floyd算法和dijkstra算法。

稠密图用prime, 稀疏图用kruskal

构造最小生成树

一般使用贪心策略，有prime算法和kruskal算法

Prime 算法 算法复杂度O(E + V log V) if you use a fibonacci heap

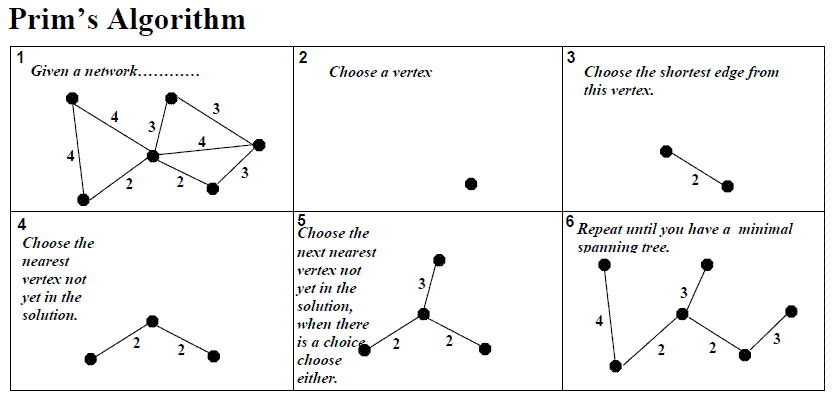
• 清空生成树，任取一个顶点加入生成树

• 在那些一个端点在生成树里，另一个端点不在生成树里的边中，选取一条权最小的边，将它和另一个端点加进生成树

• 重复步骤2，直到所有的顶点都进入了生成树为止，此时的生成树就是最小生成树

int prime(int cur)
{
    int index;
    int sum = 0;
    memset(visit, false, sizeof(visit));
    visit[cur] = true;
    for(int i = 0; i < m; i ++){
        dist[i] = graph[cur][i];    
    }

    for(int i = 1; i < m; i ++){

        int mincost = INF;
        for(int j = 0; j < m; j ++){
            if(!visit[j] && dist[j] < mincost){
                mincost = dist[j];
                index = j;    
            }    
        }

        visit[index] = true;
        sum += mincost;

        for(int j = 0; j < m; j ++){
            if(!visit[j] && dist[j] > graph[index][j]){
                dist[j] = graph[index][j];
            }    
        }    
    } 
    return sum;    
}

Kruskal算法

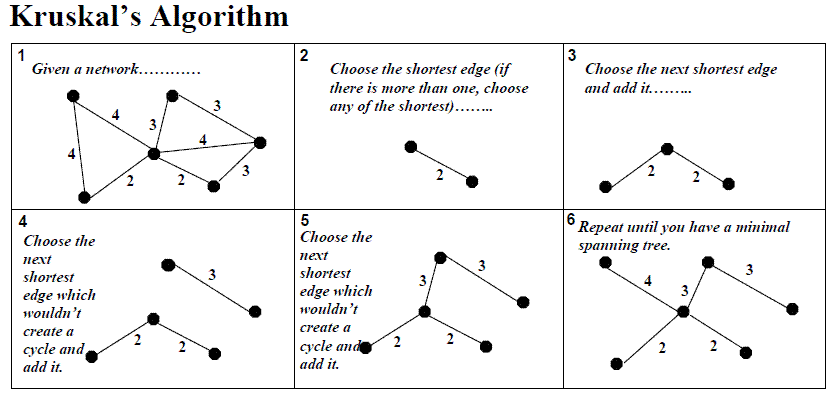
构造一个只含n个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树的根节点，则它是一个含有n棵树的森林 。之后，从网的边集中选取一条权值最小的边，若该边的两个顶点分属不同的树 ，则将其加入子图，也就是这两个顶点分别所在的 两棵树合成一棵树；反之，若该边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林只有一棵树。kruskal算法能够在并查集的基础很快的实现。结合例子来介绍具体算法实现（其中并查集的部分可以详见并查集介绍部分）

核心在由权重从小到大取边, 利用并查集find root操作找出顶点不属于同一个树的边, 进行union操作

Prime 和KrusKal最大的不同是选边的时候，prime 选的边总是维护一个连接的components，而总是选择最小的每次连接两个不同components的边.

复杂度:max(O(ElogE) , O(ElogV))

//合并x,y所在的两个集合：利用Find_Set找到其中两个
//集合的祖先，将一个集合的祖先指向另一个集合的祖先。
void Union(int x, int y)
{
    x = find_set(x);    
    y = find_set(y);
    if(x == y){
        return ;    
    }
    if(rank[x] < rank[y]){
        father[x] = find_set(y);    
    }
    else{
        if(rank[x] == rank[y]){
            rank[x] ++;    
        }    
        father[y] = find_set(x);
    }
    return ;
}

bool cmp(pnode a, pnode b)
{
    return a.val < b.val;    
}

int kruskal(int n) //n为边的数量 
{
    int sum = 0;
    make_set();
    for(int i = 0; i < n; i ++){   //从权最小的边开始加进图中 
        if(find_set(edge[i].start) != find_set(edge[i].end)){
            Union(edge[i].start, edge[i].end);
            sum += edge[i].val;    
        }    
    }
    return sum;    
}

http://www.lintcode.com/en/problem/minimum-spanning-tree/

Minimum Spanning Tree

给十几个城市供电，连接不同城市的花费不同，让花费最小同时连到所有的边。给出一系列connection类，里面是edge两端的城市名和它们之间的一个cost，找出要你挑一些边，把所有城市连接起来并且总花费最小。不能有环，最后所以城市要连成一个连通块。
不能的话输出空表，最后还要按城市名字排序输出，按照node1来排序,如果一样的话再排node2。