5/10, Tree，修改结构

Flatten Binary Tree to Linked List

很符合递归思想的写法，美中不足是每次都要把左子树遍历一遍好去找尾端节点，如果整个树左子树体积非常大而右子树很小的话，时间复杂度会很高。最差的情况是，整个树是一个只有左边的链表，时间复杂度可以达到 O(n^2)，而且用递归还要花费栈空间。

public class Solution {
    public void flatten(TreeNode root) {
        if(root == null) return;

        flatten(root.left);
        flatten(root.right);

        TreeNode left = root.left;
        TreeNode right = root.right;

        root.left = null;
        root.right = left;
        while(root.right != null){
            root = root.right;
        }
        root.right = right;
    }
}

于是这题有特别赞的O(n)时间O(1)空间写法，还是利用 Morris 遍历。

Morris 遍历的特点是寻找左子树中能沿着右边走最长的节点，并且利用这个节点做文章；这题是把 right 指针直接指向 root 的右节点了，相当于每次缩进去【root.left -> 左子树最长向右路径】这段到右子树上，如此反复。因此省去了最坏情况下重复遍历寻找链表尾的过程。

public class Solution {
    public void flatten(TreeNode root) {
        TreeNode cur = root;
        while(cur != null){
            if(cur.left == null){
                cur = cur.right;
            } else {
                TreeNode prev = cur.left;
                while(prev.right != null){
                    prev = prev.right;
                }
                prev.right = cur.right;
                cur.right = cur.left;
                cur.left = null;
            }
        }
    }
}

Reverse LinkedList

链表经典水题，把它放在这是因为它和下一题真的很像，只是维度上更单一而已。

public class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        while(head != null){
            ListNode temp = head.next;
            head.next = prev;
            prev = head;
            head = temp;
        }
        return prev;
    }
}

Binary Tree Upside Down

这题与其说是 Tree 类题目，不如说更像 LinkedList... 因为有很多的存 temp 和改动 reference ptr 的过程，尤其是迭代版，活脱一个反转列表。

• 迭代版

public TreeNode upsideDownBinaryTree(TreeNode root) {
    TreeNode curr = root;
    TreeNode temp = null;
    TreeNode prev = null;

    while(curr != null) {
        TreeNode next = curr.left;
        curr.left = temp;
        temp = curr.right;
        curr.right = prev;

        prev = curr;
        curr = next;
    }
    return prev;
}

• 递归版

public TreeNode upsideDownBinaryTree(TreeNode root) {
    if(root == null || root.left == null) {
        return root;
    }

    TreeNode newRoot = upsideDownBinaryTree(root.left);
    root.left.left = root.right;   // node 2 left children
    root.left.right = root;         // node 2 right children
    root.left = null;
    root.right = null;
    return newRoot;
}

(FB) BST to doubly linked-list

LC 论坛的讨论帖http://articles.leetcode.com/convert-binary-search-tree-bst-to/

递归

思路 ：http://www.geeksforgeeks.org/convert-given-binary-tree-doubly-linked-list-set-3/

• 完全就是 in - order 的递归结构，左-中-右

• 核心在于 “中” 这步上，如何正确做好 “拼接” 工作

• 我们需要存一个全局变量 prev 用于保存 "左子树的最后一个节点"，在每步上，和 root 做双向拼接； prev 初始化为 null;

• 额外用于遍历 LinkedList 还需要存下 head ; 在 prev 为 null 的时候 root 就代表着最左面的节点，设一下就好，之后就不用管了。

时间复杂度 O(n).

private static class TreeNode{
        int val;
        TreeNode left,right;
        public TreeNode(int val){
            this.val = val;
        }
    }

    static TreeNode prev;
    static TreeNode head;

    // In-order
    public static void convert(TreeNode root){
        if(root == null) return;

        convert(root.left);

        if(prev == null){
            head = root;
        } else {
            root.left = prev;
            prev.right = root;
        }
        prev = root;

        convert(root.right);

    }

    public static void main(String[] args){

        TreeNode node1 = new TreeNode(1);
        TreeNode node2 = new TreeNode(2);
        TreeNode node3 = new TreeNode(3);
        TreeNode node4 = new TreeNode(4);
        TreeNode node5 = new TreeNode(5);
        TreeNode node6 = new TreeNode(6);
        TreeNode node7 = new TreeNode(7);
        TreeNode node8 = new TreeNode(8);
        TreeNode node9 = new TreeNode(9);
        TreeNode node10 = new TreeNode(10);

        node2.left = node1;
        node2.right = node3;
        node4.left = node2;
        node4.right = node5;
        node6.left = node4;
        node6.right = node9;
        node9.left = node8;
        node8.left = node7;
        node9.right = node10;

        convert(node6);

        while(head != null){
            System.out.print(" " + head.val);
            head = head.right;
        }
    }

迭代(Stack)

• In-order 跑一遍，每次 pop 出来的时候，我们就有 root 了；

• 然后拼接的逻辑处理和递归的方法完全一样，这次连全局变量都不用，简单直接~

时间O(n)，空间 O(log n)

  // In-order
    public static TreeNode convert(TreeNode root){
        if(root == null) return null;

        TreeNode prev = null;
        TreeNode head = null;

        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while(!stack.isEmpty() || cur != null){
            while(cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode node = stack.pop();

            if(prev == null){
                head = node;
            } else {
                prev.right = node;
                node.left = prev;
            }

            prev = node;
            cur = node.right;
        }
        return head;
    }

    public static void main(String[] args){

        TreeNode node1 = new TreeNode(1);
        TreeNode node2 = new TreeNode(2);
        TreeNode node3 = new TreeNode(3);
        TreeNode node4 = new TreeNode(4);
        TreeNode node5 = new TreeNode(5);
        TreeNode node6 = new TreeNode(6);
        TreeNode node7 = new TreeNode(7);
        TreeNode node8 = new TreeNode(8);
        TreeNode node9 = new TreeNode(9);
        TreeNode node10 = new TreeNode(10);

        node2.left = node1;
        node2.right = node3;
        node4.left = node2;
        node4.right = node5;
        node6.left = node4;
        node6.right = node9;
        node9.left = node8;
        node8.left = node7;
        node9.right = node10;

        TreeNode head = convert(node6);

        while(head != null){
            System.out.print(" " + head.val);
            head = head.right;
        }
    }

Convert DLL back to BST

http://algorithms.tutorialhorizon.com/convert-a-sorted-doubly-linked-list-to-balanced-bst/

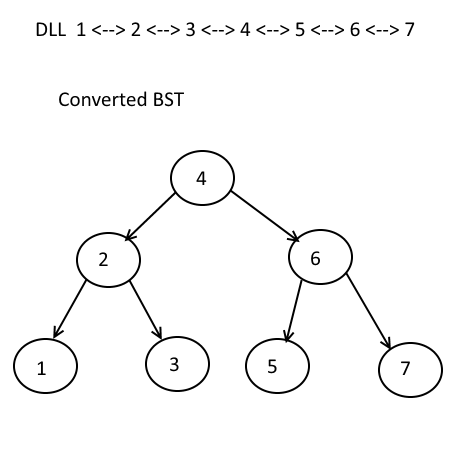
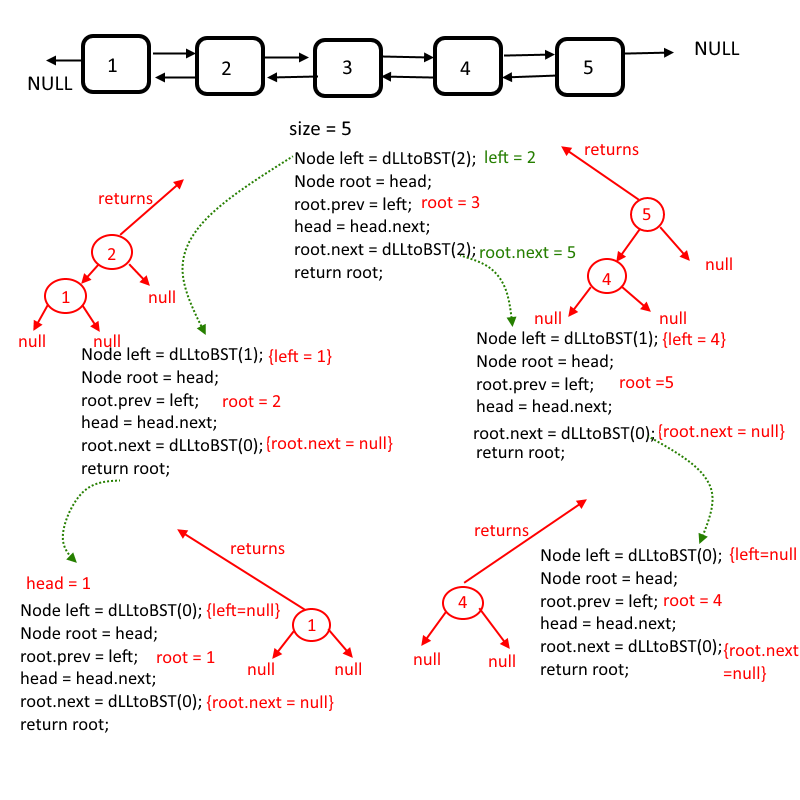
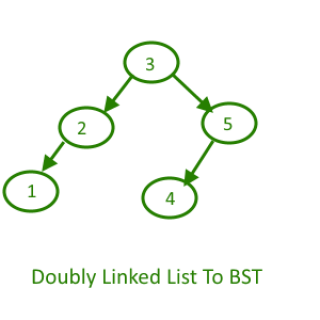
核心在递归node两边, head节点总指向当前root节点

    static Node headc = firstnode;
    //convert double link list back to tree
    //http://algorithms.tutorialhorizon.com/convert-a-sorted-doubly-linked-list-to-balanced-bst/
    private static Node convertback(int size) {
        // TODO Auto-generated method stub
        if(size<=0)
            return null;
        Node left = convertback(size/2);
        Node root = headc;
        root.left = left;
        headc = headc.right;
        Node right = convertback(size-(size)/2-1);
        root.right = right;
        return root;
    }

Add One Row to Tree

d==1特殊处理，否则到d－2层，添加children，将原children设为孙子。

public TreeNode addOneRow(TreeNode root, int v, int d) {
        if (d == 1) {
            TreeNode newroot = new TreeNode(v);
            newroot.left = root;
            return newroot;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        for (int i = 0; i < d-2; i++) {
            int size = queue.size();
            for (int j = 0; j < size; j++) {
                TreeNode t = queue.poll();
                if (t.left != null) queue.add(t.left);
                if (t.right != null) queue.add(t.right);
            }
        }
        while (!queue.isEmpty()) {
            TreeNode t = queue.poll();
            TreeNode tmp = t.left;
            t.left = new TreeNode(v);
            t.left.left = tmp;
            tmp = t.right;
            t.right = new TreeNode(v);
            t.right.right = tmp;
        }
        return root;
    }

public TreeNode addOneRow(TreeNode root, int v, int d) {
        if (d < 2) {
            TreeNode newroot = new TreeNode(v);
            if (d == 0) newroot.right = root;
            else newroot.left = root;
            return newroot;
        }
        if (root == null) return null;
        root.left = addOneRow(root.left, v, d == 2 ? 1 : d-1);
        root.right = addOneRow(root.right, v, d == 2 ? 0 : d-1);
        return root;
    }