6/1 Tree,子树结构
需要检查子树结构的题都需要一个 helper 函数,带着两个 root,递归解决。 如果默认没给,就自己写一个。
子树类问题如果出现不连续,或者需要多个子树信息的时候,自定义 SubtreeTuple 是最合适的选择。
subtree size (int);
在 size / count 这种非负情况下,还可以把符号当 flag 用;
subtree min/max (int);
这种递归结构中先处理完 left / right 再来汇总结果的,其实就是 post-order traversal. 这点在 search 类 dfs 中也很常见,比如安卓解锁,数解锁方式数量的做法。
Tree 类问题另一个递归转迭代的思路就是,观察下递归是 pre-order, in-order 还是 post-order,然后对应的靠 stack 保存状态,模拟整个过程即可。
Same Tree
Trivial problem.
public class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == q) return true;
if(p == null || q == null) return false;
if(p.val != q.val) return false;
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}
迭代写法,思路很简单,就是按照同一个顺序做 DFS (pre-order),每步上检查下元素值和 stack 大小就行,如果两个树一样,那么在迭代过程中所有的状态也都应该是一样的。
敲黑板重点, 判断stack状态一致通过判断每次pop出的value和压入left right node后, 栈的大小.
这个写法的子树访问路线以及顺序,和递归的写法是完全一样的。也就是说,其实这个迭代写法的思路,是完全建立在递归写法的代码上:
递归中先对两个 root 判断 (中)
然后递归处理两棵子树:
先左,后右;
这就是 pre-order 嘛。
public boolean isSameTree(TreeNode p, TreeNode q) {
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
if(p != null) stack1.push(p);
if(q != null) stack2.push(q);
while(!stack1.isEmpty() && !stack2.isEmpty()){
TreeNode node1 = stack1.pop();
TreeNode node2 = stack2.pop();
// Check cur
if(node1.val != node2.val) return false;
// Add Next
if(node1.right != null) stack1.push(node1.right);
if(node2.right != null) stack2.push(node2.right);
if(stack1.size() != stack2.size()) return false;
if(node1.left != null) stack1.push(node1.left);
if(node2.left != null) stack2.push(node2.left);
if(stack1.size() != stack2.size()) return false;
}
return stack1.size() == stack2.size();
}
Subtree of Another Tree
开始用了暴力递归, 实际上一个一个pre order traversal, 查string就可以了.
public class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
if(s==null && t==null) return true;
if(s==null||t==null) return false;
if(isSubtree(s.left, t))
return true;
if(isSubtree(s.right, t))
return true;
if(isSame(s, t))
return true;
return false;
}
public boolean isSame(TreeNode s, TreeNode t){
if(s==null && t==null) return true;
if(s==null||t==null) return false;
if(s.val==t.val)
return isSame(s.left, t.left) && isSame(s.right, t.right);
return false;
}
}
preorder
public class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
String spreorder = generatepreorderString(s);
String tpreorder = generatepreorderString(t);
return spreorder.contains(tpreorder) ;
}
public String generatepreorderString(TreeNode s){
StringBuilder sb = new StringBuilder();
Stack<TreeNode> stacktree = new Stack();
stacktree.push(s);
while(!stacktree.isEmpty()){
TreeNode popelem = stacktree.pop();
if(popelem==null)
sb.append(",#"); // Appending # inorder to handle same values but not subtree cases
else
sb.append(","+popelem.val);
if(popelem!=null){
stacktree.push(popelem.right);
stacktree.push(popelem.left);
}
}
return sb.toString();
}
}
Symmetric Tree
这题和上一题非常像,都是给你两个 root,去判断他们的结构,考虑到要做 symmetric tree 所以每次递归的时候参数是 p.left 和 q.right ,而不是每次都同一方向。
public class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return isSymmetric(root.left, root.right);
}
private boolean isSymmetric(TreeNode p, TreeNode q){
if(p == q) return true;
if(p == null || q == null) return false;
if(p.val != q.val) return false;
return isSymmetric(p.left, q.right) && isSymmetric(p.right, q.left);
}
}
Bonus : 用迭代。
这题用迭代的写法和思路,思路像 google onsite 面经里出现过的,交替输出 kth level 的节点。 Queue(deque) 的写法很好写,空间优化上就需要用 push 顺序相反的两个 stack 了。
具体思路参考了下论坛,我当初的写法是用两个 queue 存两个 level,对于每个 level 用类似 two pointer 的方式去检查元素,不过因为 queue 的大小一直变动,而且 queue 的 implementation 直接 access by index 也不太方便,写起来很麻烦。
比较好的思路是根据题意,直接把每个 level 拆成两个 queue,像 segment tree 似的,一个 queue 对应左子树,一个 queue 对应右子树,插入的时候,如果 q1 放左节点,q2 就放右节点,vice versa. 如果结果正确的话,两个 queue 里面的元素完全一样。
通过check null value保证结构是一样的.
public class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
Queue<TreeNode> q1 = new LinkedList<TreeNode>();
Queue<TreeNode> q2 = new LinkedList<TreeNode>();
evalAndAdd(root, root, q1, q2);
while(!q1.isEmpty()){
int size = q1.size();
for(int i = 0; i < size; i++){
TreeNode n1 = q1.poll();
TreeNode n2 = q2.poll();
if(!evalAndAdd(n1.left, n2.right, q1, q2)) return false;
if(!evalAndAdd(n1.right, n2.left, q1, q2)) return false;
}
}
return true;
}
private boolean evalAndAdd(TreeNode n1, TreeNode n2, Queue<TreeNode> q1, Queue<TreeNode> q2){
if(n1 == null && n2 == null) return true;
if(n1 == null || n2 == null) return false;
if(n1.val == n2.val){
q1.offer(n1);
q2.offer(n2);
return true;
}
return false;
}
}
同样一题,用 stack 省空间的做法,其实和两个 queue 的思路基本完全一样。。
两种做法都是把树 traverse 了一遍,只不过顺序不同。有的时候我觉得,各种 tree 的 traversal,其实就像花式 for loop 一个 array 一样。
这题的双 stack 代码和 Same Tree 基本一样,只是 push 顺序不同而已。其代码的相似与不同可以追溯到各自的递归解法中,Tree 类问题递归结构是迭代写法的指引。
stack.pop时候检查值是否一样, null不push进入, 检查每个state的size, 判断结构是否一样.
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
stack1.push(root);
stack2.push(root);
while(!stack1.isEmpty() && !stack2.isEmpty()){
TreeNode node1 = stack1.pop();
TreeNode node2 = stack2.pop();
if(node1.val != node2.val) return false;
if(node1.left != null) stack1.push(node1.left);
if(node2.right != null) stack2.push(node2.right);
if(stack1.size() != stack2.size()) return false;
if(node1.right != null) stack1.push(node1.right);
if(node2.left != null) stack2.push(node2.left);
if(stack1.size() != stack2.size()) return false;
}
return stack1.size() == stack2.size();
}
Largest BST Subtree
这题和Binary Tree Maximum Path Sum的联系非常密切,要一起研究。
这题因为执着于用一个 helper 函数同时做 “验证BST” 和 “数子树大小”的工作,做了很多次失败提交。
需要传递的信息太多就自定义 SubtreeTuple
同时这题的定义也稍微有点模糊,正确定义是:如果整棵树都是 BST,那么返回 tree size; 反之返回左右子树的最大 size ,而不考虑 root. 这个 “不考虑root” 稍微有点歧义,因为如果右子树不是 BST,左子树是 BST,并且 root.val 大于左子树的情况下,按理讲算上 root 也是一个 BST 的,只是这题我们不考虑而已。+
假如我们只用一个返回 int 的函数来层层递归,需要处理这些问题:
- 正解的的子树很可能和 root 以及上层的 node 不是连续的;
- 如果某个子树不是 BST (size = 0),也意味着上层的所有 node 都不能包含这个子树;
- 给定 root,要验证这个 root 是否在合理的左右子树极值区间内;
这些问题都不是一个 int 就能完美解决的。
时间复杂度 O(n log n),一次检查 BST/getSize 为O(n),最多重复调用 O(log n) 次
public class Solution {
public int largestBSTSubtree(TreeNode root) {
if(root == null) return 0;
if(isBST(root, null, null)) return getSize(root);
return Math.max(largestBSTSubtree(root.left), largestBSTSubtree(root.right));
}
private boolean isBST(TreeNode root, Integer min, Integer max){
if(root == null) return true;
if(min != null && root.val <= min) return false;
if(max != null && root.val >= max) return false;
return isBST(root.left, min, root.val) && isBST(root.right, root.val, max) ;
}
private int getSize(TreeNode root){
if(root == null) return 0;
return getSize(root.left) + getSize(root.right) + 1;
}
}
自定义 SubtreeTuple 的写法:
自底向上连续传递的只有 size,代表这个 tree 下面最大的 BST subtree size.
size 的绝对值代表以这个 node 为 tree root 的最大 BST subtree 大小;
size 的符号代表到底是不是 BST.
当我们有一个一定非负的变量时(在这里是 size),符号就成了 boolean 一样的可利用信息。
时间复杂度 O(n),每个 node 只访问一次,没有重复递归调用。
public class Solution {
private class SubtreeTuple{
// size of tree, negative value to reprensent invalid BST
int size;
// subtree min / max value
int min;
int max;
public SubtreeTuple(int size, int min, int max){
this.size = size;
this.min = min;
this.max = max;
}
}
public int largestBSTSubtree(TreeNode root) {
return Math.abs(helper(root).size);
}
private SubtreeTuple helper(TreeNode root){
if(root == null) return new SubtreeTuple(0, Integer.MAX_VALUE, Integer.MIN_VALUE);
SubtreeTuple left = helper(root.left);
SubtreeTuple right = helper(root.right);
if(left.size < 0 || root.val <= left.max || right.size < 0 || root.val >= right.min){
return new SubtreeTuple(Math.max(Math.abs(left.size), Math.abs(right.size)) * -1,
Math.min(left.min, root.val), Math.max(right.max, root.val));
} else {
// current left + right + root is a valid BST
return new SubtreeTuple(left.size + right.size + 1,
Math.min(root.val, left.min),
Math.max(root.val, right.max));
}
}
}
自己写的方法, 两次AC, 记得判断validBST的时候, 和validBST那题自顶向下传有效区间不同, 这个题加root可能不是validBST, 只算subtree是validBST; 判断validBST的时候不能只判断与leftchild.val和rightchild.val的关系, 需要判断leftchild.max和rightchild.min的关系, 否则[3,2,4,null,null,1] 返回是4, 正解是2
public class Solution {
int ans = 0;
class Entity{
int num;
boolean valid;
int min;
int max;
public Entity(int num, boolean valid){
this.num = num;
this.valid = valid;
}
}
public int largestBSTSubtree(TreeNode root) {
isValid(root, Integer.MIN_VALUE, Integer.MAX_VALUE);
return ans;
}
public Entity isValid(TreeNode root, int low, int high){
if(root==null){
return new Entity(0, true);
}
Entity left = isValid(root.left, low, root.val);
Entity right = isValid(root.right, root.val, high);
if(left.valid&&right.valid){
if((root.left==null || (root.val>left.max)) && (root.right==null||root.val<right.min)){
//System.out.println(root.val + " " + low + " "+high);
if(left.num+right.num+1>ans) ans = left.num+right.num+1;
Entity e = new Entity(left.num+right.num+1,true);
e.min = left.num==0?root.val:left.min;
e.max = right.num==0?root.val:right.max;
return e;
}
}
return new Entity(0,false);
}
}
Count Univalue Subtrees
对于 subtree 特征以及 flag 的处理上,和上一道题可以用完全一样的套路。
唯一的不同在于,我们要返回的是总数,而不是 max ,所以要左右加一起才行。
public class Solution {
int max = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
int ans = dfs(root);
return Math.max(max, ans);
}
public int dfs(TreeNode root){
if(root==null) return 0;
int left = Math.max(0, dfs(root.left));
int right = Math.max(0, dfs(root.right));
int sum = left+right+root.val;
max = Math.max(sum, max);
return Math.max(left, right)+root.val;
}
}
Count Complete Tree Nodes
如果一个 Tree 是 complete tree,那所有的 subtree 也都是 complete tree.
直接扫肯定 TLE .. 要利用好 complete tree 的定义和性质。
参考了一下论坛之后,写了这个解居然也 TLE,都 O(log n * log n) 了
能 AC 的代码是论坛上的这个:
public class Solution {
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
int l = leftHeight(root.left);
int r = leftHeight(root.right);
if (l == r) { // left side is full
return countNodes(root.right) + (1<<l);
}
return countNodes(root.left) + (1<<r);
}
private int leftHeight(TreeNode node) {
int h = 0;
while (node != null) {
h++;
node = node.left;
}
return h;
}
}
如果一个 Tree 是 complete tree,那所有的 subtree 也都是 complete tree.
1 << l 其实包含了每一层上加一(root) 的步骤。
按照这个代码的执行方式,每一次的左右子树必定有一个是 prefect tree,于是可以根据 depth 决定下一步处理哪棵。
public class Solution {
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
int l = leftHeight(root.left);
int r = leftHeight(root.right);
if (l == r) { // left side is full
return countNodes(root.right) + (1<<l);
}
return countNodes(root.left) + (1<<r);
}
private int leftHeight(TreeNode node) {
int h = 0;
while (node != null) {
h++;
node = node.left;
}
return h;
}
}
论坛高票解释
The height of a tree can be found by just going left. Let a single node tree have height 0. Find the heighthof the whole tree. If the whole tree is empty, i.e., has height -1, there are 0 nodes.
Otherwise check whether the height of the right subtree is just one less than that of the whole tree, meaning left and right subtree have the same height.
- If yes, then the last node on the last tree row is in the right subtree and the left subtree is a full tree of height h-1. So we take the 2^h-1 nodes of the left subtree plus the 1 root node plus recursively the number of nodes in the right subtree.
- If no, then the last node on the last tree row is in the left subtree and the right subtree is a full tree of height h-2. So we take the 2^(h-1)-1 nodes of the right subtree plus the 1 root node plus recursively the number of nodes in the left subtree.
Since I halve the tree in every recursive step, I have O(log(n)) steps. Finding a height costs O(log(n)). So overall O(log(n)^2).
注意root为null时高度为-1
public class Solution {
public int countNodes(TreeNode root) {
if(root==null) return 0;
int left = getHeight(root.left);
int right = getHeight(root.right);
if(left==right){
return (1<<(left+1))+countNodes(root.right);
}
else
return countNodes(root.left)+(1<<(right+1));
}
public int getHeight(TreeNode root){
return root==null?-1:getHeight(root.left)+1;
}
}
(G) 面经
http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=197372&highlight=google
Given a binary tree, find if there are two subtrees that are the same. (i.e. the tree structures are the same; the values on all corresponding nodes are the same). You should find the largest subtree and don’t use brute force.
贴个自己的思路,preorder serialize这个树, [5,9,2,#,#,7,3,#,#,#, 12, 10, #, #, 9, 2, #, #, 7, 3, #, #, # ]
在字符串数组中找longest repeating and non-overlapping string 就是最大identical子树。
这篇 paper 值得一看,关于 tree / subtree isomorphism
贴个 hx 的思路,仔细讨论和思考之后觉得靠谱。
假设identical的子树share一个group id. NULL的group id是0.其它子树的group id按照group在后序遍历中第一次出现的时间顺序决定。 这样我们可以一边后序遍历子树,一边建两个hashmap:+
(root value, group id of left, group id of right) -> group id of root group id -> subtrees of this group
这样我们做一遍后序遍历同时维护层数最高、subtree数量>=2的group id就行了。
这个其实跟用整棵子树的serialization作为key做法差不多,只是对key作了压缩。
如果只是要 size 的话,一个 hashmap 就够。
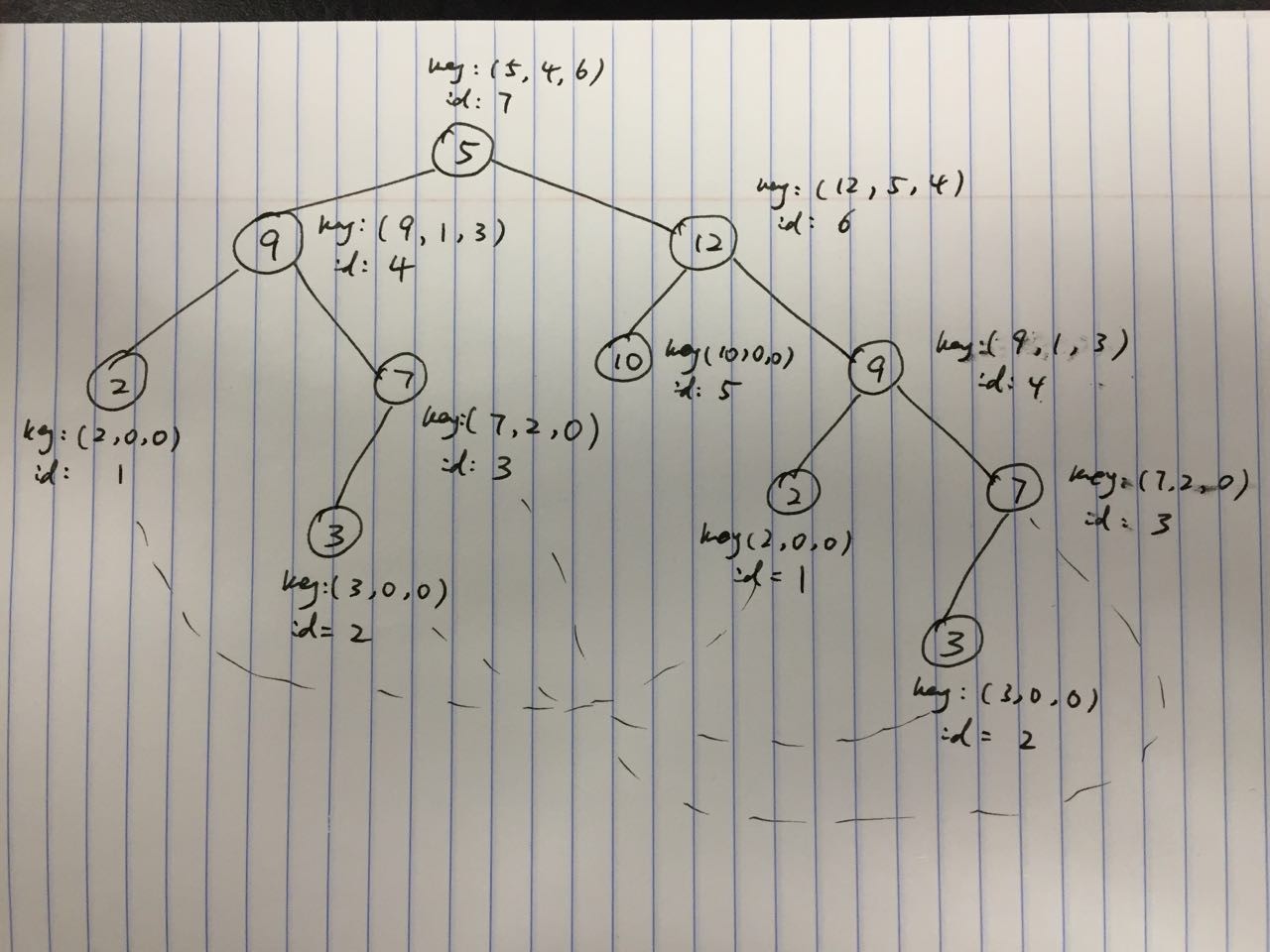
按着这个思路试着写了一下,附带两个 test case,返回的是最大 subtree 的 size.
第一个 comment 掉的 test case 和图里的一样,返回 4 .
第二个是左右完全一样的 binary tree,中间缺一个 leaf node,返回 6.
public class Solution {
private static class TreeNode{
int val;
TreeNode left, right;
public TreeNode(int val){
this.val = val;
}
}
private static class TreeTuple{
String key;
int id;
int size;
public TreeTuple(String key, int id, int size){
this.key = key;
this.id = id;
this.size = size;
}
}
public static int largestSubtree(TreeNode root){
HashMap<String, Integer> keyMap = new HashMap<>();
HashMap<Integer, List<TreeTuple>> groupMap = new HashMap<>();
int[] id = new int[1];
id[0] = 1;
postOrder(root, keyMap, groupMap, id);
Iterator<Integer> iter = groupMap.keySet().iterator();
int maxSize = 0;
while(iter.hasNext()){
int groupId = iter.next();
List<TreeTuple> list = groupMap.get(groupId);
if(list.size() > 1) maxSize = Math.max(maxSize, list.get(0).size);
}
return maxSize;
}
// keyMap : Key - String - (val, leftId, rightId)
// Val - Integer - groupId
// groupMap : Key - Integer - groupId
// Val - Integer - number of occurrances
private static TreeTuple postOrder(TreeNode root, HashMap<String, Integer> keyMap,
HashMap<Integer, List<TreeTuple>> groupMap, int[] id){
if(root == null) return new TreeTuple("0,0,0", 0, 0);
TreeTuple left = postOrder(root.left, keyMap, groupMap, id);
TreeTuple right = postOrder(root.right, keyMap, groupMap, id);
int curId;
TreeTuple curTuple;
String key = "" + root.val + "," + left.id + "," + right.id;
if(!keyMap.containsKey(key)){
curId = id[0]++;
keyMap.put(key, curId);
groupMap.put(curId, new ArrayList<>());
curTuple = new TreeTuple(key, curId, left.size + right.size + 1);
groupMap.get(curId).add(curTuple);
} else {
curId = keyMap.get(key);
curTuple = new TreeTuple(key, curId, left.size + right.size + 1);
groupMap.get(curId).add(curTuple);
}
return curTuple;
}
public static void main(String[] args) {
/*
TreeNode root = new TreeNode(5);
TreeNode root2 = new TreeNode(9);
TreeNode root3 = new TreeNode(2);
TreeNode root4 = new TreeNode(7);
TreeNode root5 = new TreeNode(3);
TreeNode root6 = new TreeNode(12);
TreeNode root7 = new TreeNode(10);
TreeNode root8 = new TreeNode(9);
TreeNode root9 = new TreeNode(2);
TreeNode root10 = new TreeNode(7);
TreeNode root11 = new TreeNode(3);
root.left = root2;
root.right = root6;
root2.left = root3;
root2.right = root4;
root4.left = root5;
root6.left = root7;
root6.right = root8;
root8.left = root9;
root8.right = root10;
root10.left = root11;
*/
TreeNode root = new TreeNode(0);
TreeNode rootl2 = new TreeNode(1);
TreeNode rootr3 = new TreeNode(1);
TreeNode rootl4 = new TreeNode(2);
TreeNode rootr5 = new TreeNode(2);
TreeNode rootl6 = new TreeNode(3);
TreeNode rootr7 = new TreeNode(3);
TreeNode rootl8 = new TreeNode(4);
TreeNode rootr9 = new TreeNode(4);
TreeNode rootl10 = new TreeNode(5);
TreeNode rootr11 = new TreeNode(5);
TreeNode rootl12 = new TreeNode(6);
TreeNode rootr13 = new TreeNode(6);
root.left = rootl2;
root.right = rootr3;
rootl2.left = rootl4;
rootl2.right = rootl6;
rootl4.left = rootl8;
rootl4.right = rootl10;
rootl6.right = rootl12;
rootr3.left = rootr5;
rootr3.right = rootr7;
rootr5.left = rootr9;
rootr5.right = rootr11;
rootr7.right = rootr13;
System.out.println(largestSubtree(root));
}
}